When the AI hype was reaching it’s peak I felt quite often challenged to justify my reasoning for thinking it was cool. Suddenly something I had been following for a few years and would annoy people about over drinks was now me buying into the hype. This was frustrating (yes, I liked LLMs before it was cool). However, needing to justify it so many times meant coming up with a succinct answer.
LLMs have some understanding (albeit flawed) of the fuzziest concepts we know. The human world. Something computers have been famously bad at until literally just the past few years.
Whenever people come up with a terrible app idea, a very common thing standing in the way was you’d need the computer to somehow make sense of a very fuzzy human concept, something people have a hard time recognizing1. There’s a lot to be said for a wide range of machine learning methods that have made these fuzzy concepts more tangible, but I do think LLMs take the cake. I don’t think it’s a coincidence that multi modal models (MMMs?) commonly use LLMs at their core and then attach vision or speech recognition or generation components.
It will take years to fully work out how useful this is, where LLMs will plateau in their reasoning and capability, how much we can optimize them and so on. Will they go the way of the plane, big, expensive, built by one of two companies and where you rent a seat and get where you want to go. Or will they be more like cars, small, personalizable, affordable, ubiquitous. Perhaps both, who knows. Anyways, if all those past app ideas were held back by an understanding of the fuzzy and abstract, I’d better test that idea and build something I thought could only be done with the fuzzy and the abstract.
What’s the most dystopian thing I can imagine What’s something that’s hard and relies heavily on disparate abstract ideas?
Can I use an LLM on large amounts of conversational-ish data and rank peoples suitability for a role? Jokes aside, it is a sort of morbid curiosity that drove me to try this idea. Recruitment is extremely difficult and very unscientific. Many ideas exist: long interview processes, hire fast and fire faster, and even our friend machine learning applied on big datasets of candidate attributes (ever wonder why recruiters want you to fill out all the information that’s already in your CV you already attached?). Its big business but not because it works that well, it’s just that demand is high. If you could make some half decent system to rank people, it would probably become quite popular quite quickly. The implications of that could easily go further than recruitment. I’ll talk more about that later.
I can’t get a bunch of interview transcripts, that data probably exists but I’m lazy and I can get it something else decent instead: social media comments. I pulled 20k-ish words from 97 prolific commentators on hackernews. They talk about technical topics and news and stuff, and in twenty thousand words surely we can get a measure of a person. For this idea to work, I’m assuming that within these words is enough information to reasonably prefer one person over another for a role, if that’s not the case then this idea is never getting off the ground. It’s surely worth a shot anyways though right? The role these commentators are competing for is “Software Engineer at Google”. Yes I know I’m very creative, I didn’t even give the LLM any additional role description, in a real use case you would definitely want to do that.
How will we rank them? There exist a number of LLM leaderboards2 where people are shown two LLM outputs given the same prompt/question and asked which one they prefer. Time for some table turning! Give the LLM the comments of two people at a time and have it state a preference for one of them.
You are an LLM system that evaluates the suitability of two people for a role. You have access to their online social media comments. Often the comments may have no connection to the role. Nonetheless, state your preference for one of the candidates.
<lots and lots of comments>
Which of these two people is more suitable for the role of "Software Engineer at Google"?
Many such pairwise comparisons can be aggregated using something like the Bradley-Terry model. That might not sound familiar but if you’ve ever heard of Elo and chess ratings then you have encountered it already. Your rating is always relative to another players rating, and if you have say 800 more points than your opponent, Elo gives you a 99% chance of winning. We also get a formula for how to update ratings, which has a parameter K. I found it nice to think of this as analogous to the learning rate seen often in machine learning. In the Elo system a common value for K is 10, and all you need to know is in any matchup, your rating can at most move K points for a big difference in player ratings, and if you and your opponent have the same rating you will move K/2 points.
OK, let’s try it! I chose a first player randomly and then a second player based on a normal distribution of ratings around the first player, so that closer match ups are a little more likely. After each match we recalculate Elo ratings and go again. I used LLama3.1-instruct 70B quantized to 4 bits since that’s what will fit on my GPUs. Also, I use a little less than half of available comments, coming out to 12.5k tokens per person to keep things fast. Each comparison still takes almost 20 seconds so I run this for a while.
First problem, the model is preferring the second candidate almost all of the time!
Given that I randomized the order of person one and person two, the chance that you’d get this result coincidentally is vanishingly small. I’m pretty sure the issue is just a recency bias. The model sees person two most recently and somehow that equates to best. OK, what if we interleave each comment, one from person one, one from person two and so on?
Person one: What makes you think that?
Person two: When I was a lad I remember stories of when...
Person one: Great post! I particularly like the things and stuff
...
Notably, the comments are completely out of order and contain no additional context. I did this so that hopefully the model doesn’t spend too much time trying to work out who said what and where and in what order (and also, it was easier). Comments with quotes of other parts of responses (usually done with a > symbol) I left in, since with such a direct response I hoped the model wouldn’t be too confused by it (and again it was easier, am I rationalizing?). Anyways, did interleaving the comments help with recency bias?
Much better. In longer runs, it leveled out at about 51.5% for person one, which isn’t completely unbiased but I’m not too worried about the bias itself. What worries me is that initial bias toward person two. If the model can’t choose a good candidate just because they were described 12k tokens ago, how good could it possibly ever be at this task? If one person said something hugely decisive or important early on in the interleaved comments, would the model even remember that?3 I perhaps mitigate this slightly by shuffling the comments for each game, but still.
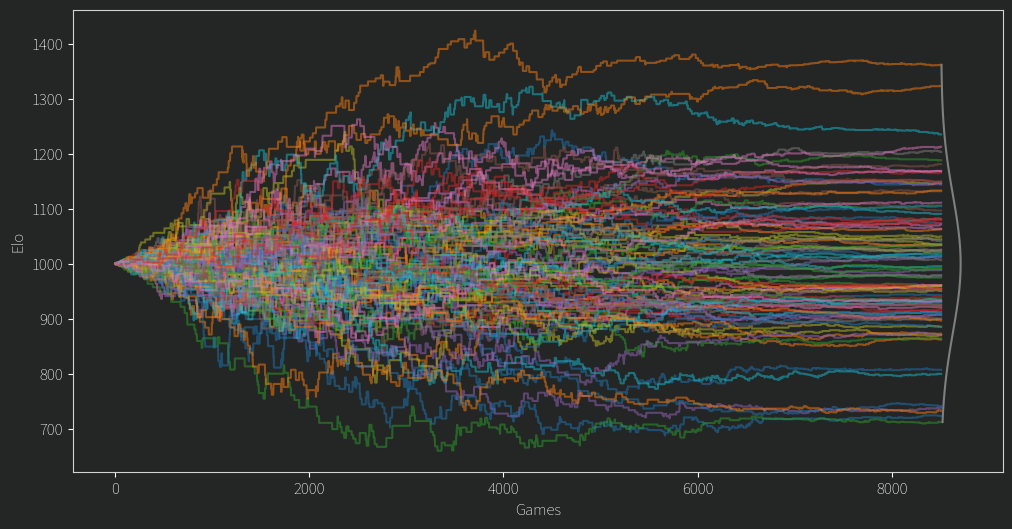
After fixing a second issue of the mean Elo dropping slowly over time (I was storing ratings as ints! Imagine!) I finally arrived at this plot. Everyone starts from an Elo of 1000 and the values diverge from there.
There are a few clear winners and losers, but for any given player in the middle of the pack, their Elo rating often seems like a random walk.
That doesn’t seem so good. Of course we might expect in the beginning an unlucky person might get matched up against a fair few stronger opponents, leading to them being unfairly under ranked until better odds give them some good match ups. However, for so many ratings to behave this way and for so long, it isn’t so promising. As for the top and bottom candidates, it turns out that if you have a propensity to comment a lot on controversial topics, you wont do so well in the rankings. The LLM gave reasoning for its choices and although I wont give specific examples it at least claims to consider things like being non confrontational and having a learning mindset and all that.
From trying out some LLM training I was often using variable learning rates, with both warmup and annealing periods. K is a bit like a learning rate right? Since we have all our pairwise comparisons we can actually rerun the whole Elo tournament in a fraction of the time (minus the Gaussian selection of competitors). With K following this curve:
I get this progression of ratings. Check it out:
Take that random walks! What justification do I have for doing this? Uhhhh Vibes, I fiddled with the start value until the largest and smallest Elo ratings seemingly reached their limits (around 1400 and 700 respectively), and the stop value such that the ratings settle down to what is hopefully their best value. The former behavior might seem counterintuitive at first, why does the largest and smallest Elo not just keep diverging as we raise K? Well, their most extreme values do, but their means will still converge on some true value representing the models confidence. As mentioned, Elo is measuring the probability of a win, and if a great candidate always beats a terrible one that should be clear in their ratings. The difference between the top (1362) and bottom (712) candidates is 650 points, and that gives the top candidate a ~98% chance of beating the lowest in a match up. Any other pair of candidates has a lower confidence.
So is this model any good? First, let’s at least convince ourselves that it has converged.
Considering all games played, how well do the Elo ratings at any given iteration predict the winners of those games? There are a total of 4656 (97 choose 2) possible pairings, and the LLM has considered 3473 of them at least once. Of those, 2115 were tested more than once (with the most tested being the two top candidates, 64 times!). “partial” wins do exist, 1326 pairings had some degree of uncertainty, i.e. at least one time the LLM preferred the first candidate and another time the second. This actually works quite well with Elo ratings, since we can take our Elo predicted win probability and compare it to the actual win ratio. Doing this over the ratings over time gives this plot:
(For those that are wondering if this is just due to annealing K, for a fixed K=32 it also converges to ~0.7 but it’s more noisy). OK, so it looks like we’ve probably converged on something, but is it any good? One thing we can look at is transitivity:
If A is better than B, and B is better than C, then A should clearly be better than C. If we take all our pairings and construct a directed graph, we can use some graph algorithms to count the number of cycles. Any cycle is automatically intransitive. Counting the number of cycles of any length is an NP-Hard problem (Yay!) but we can limit our lengths and get some reasonable answers:
Cycles of length 3: 5880
Cycles of length 4: 110728
Cycles of length 5: 2206334
Cycles of length 6: 45438450
What do these numbers mean? We can put cycles of length 3 into context by comparing them to the total number of possible triplets given the pairings available, which comes out to 62519. Doesn’t seem too bad, that’s less than 10%. If we construct a random graph of pairings we get these results:
Cycles of length 3: 15563 # ~3 times as bad
Cycles of length 4: 408633 # ~4 times as bad
Cycles of length 5: 11338193 # ~5 times as bad
Cycles of length 6: 324858266 # ~7 times as bad
Hopefully it makes sense that our performance against the random pairings gets better the longer cycles we look at, since longer cycles in a sense require our model to be more contradictory in its rankings.
What about actual performance? I can’t exactly call up each person and ask if they work for Google. Maybe I could compare it to some human based human ranking system but I don’t have that data. Indeed, without using these results and then following up with real world outcomes, it’s hard to truly know if it is any good. However, LLMs as a whole generalize quite well and their ability on a broad range of tasks for the time being improves pretty linearly with improvements to their overall loss. So, these proxies like Elo accuracy and transitivity should be at least somewhat representative. The only other thing standing in the way is the dataset. A simple example is that, even when anonymous and online, people don’t tend to reveal massive flaws or disparaging details about themselves. Some such things might still unintentionally be “present” in their writing, but measuring that seems quite unscientific. As mentioned earlier, this will work if and only if there is enough “information” in 12.5k tokens or whatever other amount of text you can obtain. I can’t fully answer that question here, so maybe this is not very inspiring.
Or perhaps it is? What would you even do with this kind of information? Zoom out, we are ranking people in a game they didn’t even sign up to play! It perhaps evokes similar feelings as one might get towards China’s social credit system or advertiser fingerprinting. We like to think that abstract and fuzzy stuff is what makes us humans special, and trying to structure it has always (and often justifiably) faced resistance. If we can use this for ranking people as candidates for work, what else might you use it for? Should we under any circumstance be reducing people to mere numbers regardless of how accurate those numbers are? That in itself is a fuzzy question, and I think needs to be considered case by case. But I do think we have a lot of such cases before us. Here, LLMs capture this fuzziness to a degree I couldn’t have imagined computers ever doing before. They may not be that good at it, but I don’t think they’ve peaked quite yet. and even so, there may be a great many fuzzy problems that current LLMs could tackle. It will take time, building such solutions still takes years even if now the tools are there for us to use.
I hope you found this post interesting. Maybe it gives you some cool ideas of (ethical please) projects you want to try. I think as new models become public, and so long as my computer doesn’t catch fire, I might revisit this and see if performance improves.
(EDIT: Read the followup to this post here)
- https://xkcd.com/1425/ ↩︎
- https://lmarena.ai/ ↩︎
- I recently read a very interesting paper which might help a lot with this sort of problem. https://arxiv.org/abs/2410.05258 ↩︎